1. INTRODUCTION
Due to climate change and the country’s expanding population, the agricultural division of India must look for more precise and effective strategies to provide a sufficient and consistent supply of food for the community while using the least amount of water possible. Measuring evapotranspiration (ET) is the most significant factor in the irrigation schedule [1,2].
Accurate estimation of ET is the first step in evaluating the water requirements of field crops [3]. Several artificial intelligence-based models are used for irrigation planning [4]. The valuation of water for crops is most important in water distributions [5]. ET0 refers to the loss of water to the surface of plants and soil [6]. Evaporation parameters are used to study water budgets, water resource management, and irrigation system design as well as to estimate plant growth and height [7]. ET plays an important role in different fields of hydrology and agriculture [2]. Precise estimation of ET0 is very important for irrigation planning, scheduling, design, and crop water management. ET is measured by various methods such as (i) Lysimetric, (ii) field experiment, (iii) water balance, and (iv) soil moisture depletion study. Lysimeters are tough and expensive to build, their operation and maintenance require particular care, and their use is restricted to specific research purpose. ET changes with climate change and as the climate has many geographical variations, the pre-developed systems have not used all available weather data and so no robust models. As a consequence of cost and difficulties in direct measurement techniques with a pyranometer and lysimeter, solar radiation and ET0 were predicted using suitable models [8]. Different empirical models have been developed for ET0 estimation rendering to various climatic conditions [9,10]. Many models such as empirical, artificial neural network, machine learning (ML), and deep learning exist in the literature to compute the global solar radiation (GSR) and ET0 [11,12]. However, the standard method recommended by the Food and Agriculture Organization (FAO), namely, the Penman-Monteith (PM-FAO56) equation requires an extensive range of data support for ET estimation. In this work, ML models with a limited number of input parameters are utilized to estimate the solar radiation and ET in chosen locations of Tamil Nadu. To estimate the ET0, the solar radiation and temperature values are used. Empirical correlations are also utilized to estimate the ET0 for comparison with ML methods. Based on the performance metrics, ML-based ET0 estimations are more accurate than empirical-based estimations. To develop the ML model, SVM and random forest algorithms are employed with a reduced number of meteorological parameters.
2. STUDY AREA AND DATA SOURCES
The study site, Coimbatore has a semi-arid tropical climate. The tomato is one of the horticultural products produced in the study location. The water requirement for tomato plant in the study location is calculated by the relation of crop coefficient and ET. The geographical parameters of the study location are given in Table 1 and Figure 1 shows the monthly average GSR and temperature values. Meteorological parameters associated with this study were obtained from India meteorological department (IMD), India and AQUASTAT tool. The measured experimental data for the estimation of GSR and ET, namely, the monthly average maximum and minimum temperature, bright sunshine duration, and daily solar radiation in kW/m2/day for 12 locations in India were obtained from IMD. Table 2 presents the measured GSR data obtained from IMD. The whole dataset is partitioned into two sets, namely, training sub-set (70%) and testing sub-set (30%). It is further processed with the assistance of empirical and ML models. The coefficients of the solar radiation empirical models are estimated with the help of a training data set and testing datasets are used to validate the models.
Table 1: Geographical parameters of the study site.
| Latitude° (n) | Longitude °(E) | Climate | Annual Solar Radiation MJ/m2/day | Average Evapotranspiration in mm/day |
|---|---|---|---|---|
| 11.02 | 76.95 | Tropical | 19.5 | 4.5 |
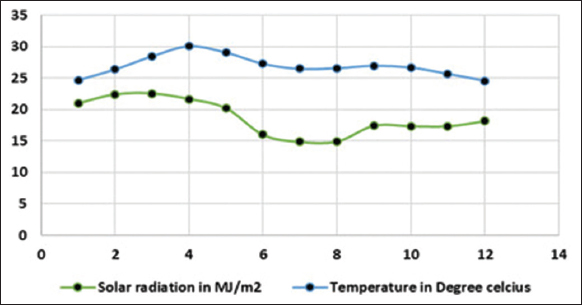 | Figure 1: Monthly average solar radiation in MJ/m2/day and temperature of the study site-Coimbatore. [Click here to view] |
Table 2: Measured monthly mean GSR in kW/m2/day for Indian Cities from IMD for training ML models.
| Months | Location/global solar radiation | |||||||
|---|---|---|---|---|---|---|---|---|
| Patna | New Delhi | Nagpur | Hyderabad | Chennai | Bhubaneswar | Mangalore | Trivandrum | |
| January | 3.3 | 3.2 | 4.3 | 5.2 | 4.7 | 4.1 | 4.9 | 4.9 |
| February | 4.2 | 4.1 | 5.2 | 5.8 | 5.8 | 4.7 | 5.6 | 5.5 |
| March | 5.2 | 5.1 | 5.8 | 6.4 | 6.2 | 5.6 | 5.5 | 5.4 |
| April | 5.7 | 5.9 | 6.5 | 6.6 | 6.3 | 6.4 | 5.9 | 5.1 |
| May | 5.7 | 5.8 | 6.6 | 6.7 | 6.0 | 6.2 | 5.2 | 4.8 |
| June | 4.8 | 5.6 | 5.2 | 5.3 | 5.6 | 4.6 | 4.9 | 4.6 |
| July | 4.0 | 4.7 | 3.8 | 4.8 | 5.1 | 4.3 | 3.6 | 4.5 |
| August | 4.5 | 4.4 | 4.0 | 4.6 | 5.2 | 4.2 | 4.0 | 4.9 |
| September | 4.1 | 4.3 | 4.9 | 4.9 | 5.2 | 4.0 | 4.8 | 5.0 |
| October | 4.1 | 4.3 | 5.1 | 5.0 | 4.6 | 4.9 | 5.1 | 4.5 |
| November | 3.6 | 3.5 | 4.4 | 5.4 | 4.0 | 4.4 | 5.0 | 4.0 |
| December | 3.2 | 2.9 | 4.1 | 5.0 | 3.7 | 3.7 | 4.9 | 4.4 |
ML: Machine learning, GSR: Global solar radiation, IMD: India meteorological department.
3. MATERIALS AND METHODS
3.1. Estimation of Reference ET
The lysimetric method is used for the direct measurement of in situ ET0 values which are considered as the only best method to get accurate estimates of ET0. However, this lysimetric method has many drawbacks associated with the high cost and difficulties in the maintenance of complex instrumentation. PM-FAO56 equation has been considered as the standard model for the estimation of ET0 for crop water requirements under different climate conditions and various time scales.
ET0 - Reference ET is given by the following equation [10].
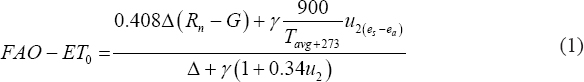 |
Where Rn is GSR in MJ m−2 d−1,
G is the soil heat flux density MJ m−2 d−1
Tavg is the average air temperature (°C)
es is the saturation vapor pressure (kPa)
ea is the actual vapor pressure (kPa)
? Is the slope of the vapor pressure (kPa°C−1)
γ is the psychrometric constant (kPa°C−1)
u2 is the wind speed in m/s.
The above equation (1) requires a huge exhaustive meteorological data set. Simpler empirical equations which require only the maximum and minimum air temperature and solar radiation data are used in this study for the estimation of ET.
3.2. Estimation of GSR Using Empirical Correlations
Empirical models are math and coefficient based. This classical statistical approach relies on the linear relationship between inputs and outputs and exists as mathematical equations. There are two sets of empirical models. The first set of models estimate solar radiation using bright sunshine hours and the second set of temperature-based models estimate the solar radiation using the minimum, maximum, and mean temperature data which is suitable for locations where the sunshine data is unavailable.
Some of the sunshine and temperature-based empirical models are shown in Table 3. Figure 2 presents the linear relationship between the solar radiation and the input weather parameters by estimating the “R” value [13]. From this, it is observed that sunshine duration and temperature received the first two ranks and are more closely correlated with GSR. Hence, sunshine duration and temperature-based empirical and ML models are selected for the estimation of GSR. Table 3 summarizes the sunshine and temperature-based empirical correlations employed for the estimation of the solar radiation. Under the empirical category, although the model performances are close to each other, the simple linear model is recommended as the optimum model due to lesser computational effort when compared with quadratic and cubic models.
Table 3: Empirical correlations used for the estimation of solar radiation.
| Sunshine models | Temperature models |
|---|---|
Linear model (S1)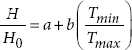 | Linear model (T1)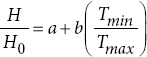 |
Quadratic model (S2)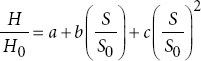 | Quadratic model (T2)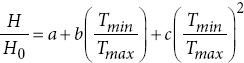 |
Cubic model (S3)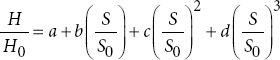 | Cubic model (T3)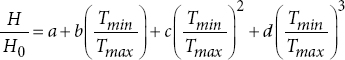 |
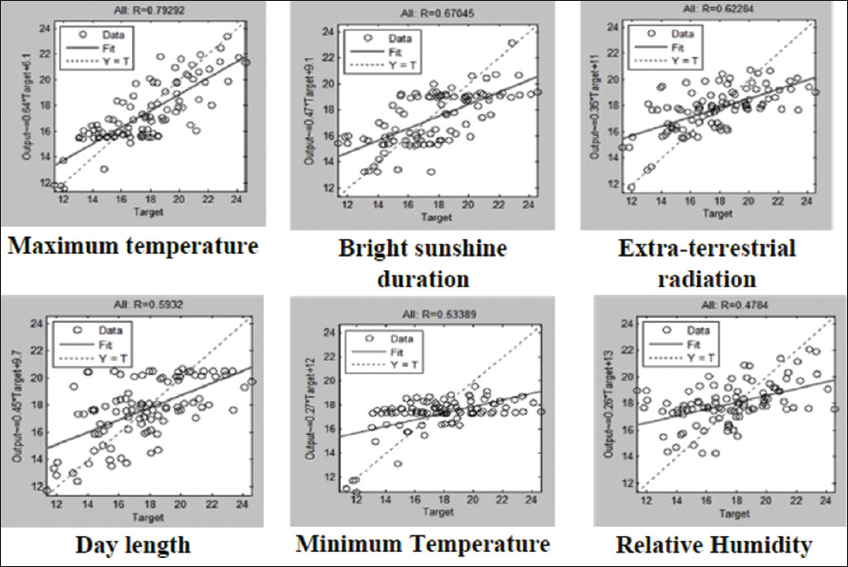 | Figure 2: Linear relationship between solar radiation and various weather parameters. [Click here to view] |
Temperature and sunshine-based empirical correlations and ML techniques such as SVM and tree-based random forest ML algorithms are used for the estimation of GSR. Spyder an open-source cross-platform integrated development environment written in python language for scientific programming is used to develop computer codes for ML models.
Various statistical indexes, namely, correlation coefficient (R), root mean squared error (RMSE), mean absolute percentage error (MAPE), and mean bias error (MBE) are used to assess the performance of the models. For better modeling accuracy RMSE, MAPE, and MBE indices should be nearer to zero, but R-value should be nearer to 1.
The MAPE shows the average absolute percentage deviation between the calculated and the actual observed GSR data and is determined by:
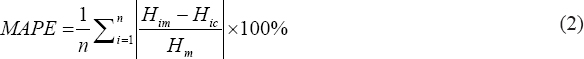 |
Information regarding the long-term performance is provided by the mean bias error. This is an indicator of the average deviation of the forecast values from the actual observed GSR values. Mean bias error is determined by:
 |
The RMSE determines the model’s accuracy by comparing the deviation between the predicted and actual GSR data. The RMSE always has a non-negative value and is computed by:
 |
Where Hi,c is the ith computed value Hi,m is the ith observed value of GSR and n is the total number of observations. The error statistics of the temperature and sunshine models are available in Table 4. From this, it is proved that the sunshine empirical models are more precise than temperature-based empirical models. Temperature models can be used in locations where sunshine records are not available.
Table 4: Performance metrics of empirical models.
| Performance indicators | Linear model | Quadratic model | Cubic model |
|---|---|---|---|
| Sunshine models | |||
| R | 0.9784 | 0.9783 | 0.9779 |
| RMSE | 0.6953 | 0.6963 | 0.6953 |
| MAPE | 0.6450 | 0.6400 | 0.6127 |
| Temperature models | |||
| R | 0.9191 | 0.9198 | 0.9217 |
| RMSE | 1.2428 | 1.2434 | 1.2318 |
| MAPE | 1.0419 | 1.0576 | 1.0559 |
RMSE: Root mean squared error, MAPE: Mean absolute percentage error.
3.3. Estimation of GSR and ET Using ML Models
ML is the division of study that gives the ability of computers to learn from huge amounts of data [14]. These ML and deep learning are contemporary technologies that can be used efficiently to predict the water requirements for agricultural crops. Accurate estimation of ET is the first step in evaluating the water requirements of field crops. Data on solar radiation are crucial for estimating ET and managing crop water. SVM and Random Forest are the two most widely utilized ML techniques for estimating solar radiation and ET. In the literature, there are also deep learning models [15] and hybrid ML models for predicting ET [16,17]. Table 5 provides a summary of ML-based methods for climate-smart agriculture approach.
Table 5: An overview of AI/ML-based Climate-smart agriculture approaches.
| Input variables | Prediction accuracy | Reference | Model | Applications |
|---|---|---|---|---|
| Solar radiation, temperature, wind speed, sunshine and altitude | RMSE–0.290 mm d−1, R2–98%. | Dimitriadou and Nikolakopoulos 2022 [22] | ANN and Penman-Monteith | ANN-based Evapotranspiration estimation. |
| Humidity and temperature | SVM RMSE–0.97 mm/day MAE–0.71 mm/day | Hu et al. 2022 [23] | SVM, KNN and ANN | Precise estimation of ET and efficient agriculture crop water management. |
| Temperature, wind speed, sunshine, humidity and GSR | MAPE-7–19% R2−0.86. | Zereg and Belouz 2023 [24] | Support Vector Regression (SVR) ML algorithm | SVR-based ET0 estimation |
| Monthly mean maximum and minimum temperature and daily Global Solar Radiation in MJ/m2/day. | RMSE−0.625 R−0.9803 | Meenal et al. 2019 [25] | Linear regression, SVM, Random Forest | Assessment of solar energy potential |
| Wind Speed, Temperature, GSR, Latent Heat, Precipitation, Relative humidity, Atmospheric Pressure | 27% reduction in water use and 40%. Increase in the yield of the crops. | Poyen et al. 2021 [26] | Fuzzy rule-based irrigation controller | Calculation of actual water loss for providing optimal irrigation for framing |
ML: Machine learning, RMSE: Root mean squared error, MAPE: Mean absolute percentage error, GSR: Global solar radiation.
Random forest ML algorithm is more suited to classification problems when compared with regression problems [18]. It creates decision trees using a variety of samples, taking into account the average in regression problems and the majority votes for classification problems. The random forest algorithm’s ability to handle both continuous and categorical variables is one of its most important characteristics. Both classification and regression analysis can be performed using SVM, which are robust supervised learning models [19,20]. Finding a hyperplane with the best decision boundary that clearly classifies the data points is the goal of the SVM algorithm. Table 6 presents the estimated solar radiation values using the ML models, namely, the random forest algorithm and SVM.
Table 6: Estimation of solar radiation in MJ/m2/day using machine learning models for the location-Coimbatore.
| Months | Random forest | SVM |
|---|---|---|
| January | 20.98 | 23.13 |
| February | 22.39 | 24.99 |
| March | 22.53 | 25.39 |
| April | 21.77 | 22.07 |
| May | 19.99 | 19.77 |
| June | 15.95 | 16.11 |
| July | 14.87 | 15.03 |
| August | 15.03 | 16.08 |
| September | 17.44 | 17.77 |
| October | 17.44 | 17.11 |
| November | 17.45 | 17.88 |
| December | 18.07 | 18.96 |
4. CROP WATER REQUIREMENT
For all major crops, the irrigation water requirement is determined as follows [21]:
Step 1: Estimate the reference crop ET: ET0
Step 2: Get the crop factors: Kc
Step 3: Compute the crop water need: ETc = ET0 × Kc
The ET0 is estimated by solar radiation-based empirical models and random forest algorithm. To estimate the ET, the solar radiation and temperature values are used. The water requirement for the crops (ETc) in millimeter/day is determined by multiplying the estimated reference crop ET and crop coefficient (kc) value.
The estimated solar radiation and the measured temperature values are used as input variables for empirical and random forest ML model to predict the ET0 value for the particular crop per day to understand how much water is required for the crop. The water requirement for the tomato crop in millimeter/day is calculated by multiplying the estimated ET and crop coefficient (kc) value. The estimated ET using empirical and random forest ML models is compared. From the results, Table 7 and Figure 3, it is observed that ET0 predictions using ML model are more precise than empirical models. Hence, the predicted ET0 value is used for agro-meteorological applications. Figure 4 shows the water requirement for the tomato crop. From the results, it was observed that the annual average solar potential of Coimbatore is around 19.69 MJ/m2/day. The reference crop ET ranges from 3.7 to 5.7 mm/day.
Table 7: Estimation of ET0 in mm/day using empirical and machine learning models for the location Coimbatore.
| Months | Empirical estimation | ML-based estimation | Satellite data |
|---|---|---|---|
| January | 5.0 | 4.4 | 4.4 |
| February | 5.2 | 4.9 | 5.0 |
| March | 5.2 | 5.6 | 5.7 |
| April | 5.1 | 5.6 | 5.7 |
| May | 4.9 | 5.0 | 5.2 |
| June | 4.2 | 4.0 | 4.1 |
| July | 4.1 | 3.7 | 3.7 |
| August | 4.1 | 3.7 | 3.8 |
| September | 4.4 | 4.0 | 4.1 |
| October | 4.4 | 3.8 | 3.8 |
| November | 4.4 | 3.7 | 3.7 |
| December | 4.6 | 4.0 | 3.8 |
ML: Machine learning, ET0: Evapotranspiration.
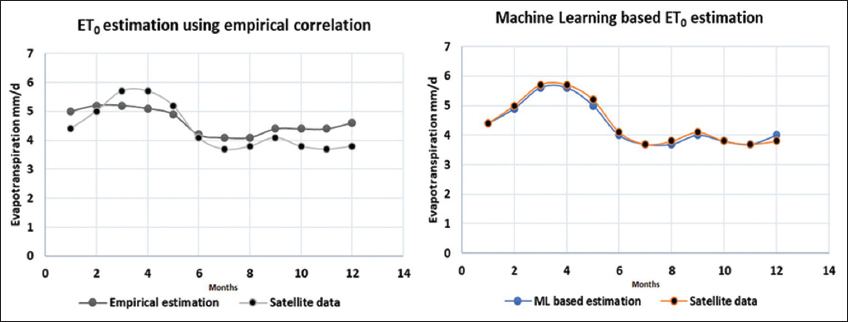 | Figure 3: Comparision between predicted evapotranspiration data using empiricaland machine learning method and satelite data for the study site: 11.0168° N latitude, 76.9558° E longitude. [Click here to view] |
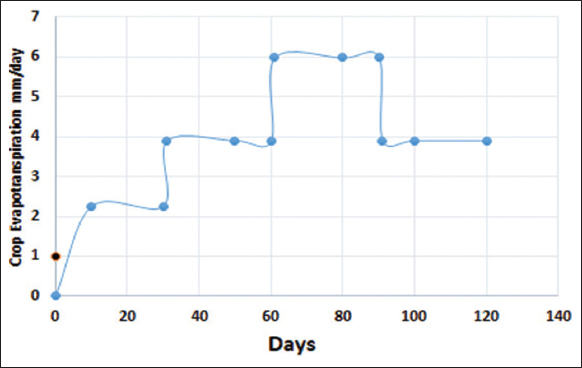 | Figure 4: Crop water need evapotranspiration in mm/day for the tomato crop. [Click here to view] |
5. CONCLUSION
Although weather prediction systems have undergone significant advancements recently, their direct applications in efficient crop water management have not been fully investigated. Here, we made an attempt to apply the ML techniques to estimate the ET through which the water requirement is calculated for the field crops in the theme of the application of weather in agriculture. Random forest ML algorithm and empirical correlations are used to predict the ET0 value for the tomato crop to understand how much water is required for the crop. The annual average solar potential of the study site is around 19.69 MJ/m2/day and ET0 value ranges from 3.7 to 5.7 mm/day. It is found that using the random forest method with reduced input variables, a better performance metrics is achieved with a less mean square error of 0.03. From the obtained results, it is observed that the solar radiation and ET0 predictions using the random forest ML model is more precise than the empirical models. Thus, ML algorithms can be attempted to estimate ET0 and the actual water requirement for the crops to increase the agricultural yield and to lower the water consumption. The findings of this study can be applied as a successful planning, design, and management strategy for irrigation as well as a solution to the existing challenges in agrometeorological applications.
6. ACKNOWLEDGMENT
We would like to thank IMD, Pune for meteorological data support.
7. FUNDING
There is no funding to report.
8. CONFLICTS OF INTEREST
The authors report no financial or any other conflicts of interest in this work.
9. ETHICAL APPROVALS
This study does not involve experiments on animals or human subjects.
10. DATA AVAILABILITY
The data are available on requesting corresponding author.
11. FUTURE SCOPE
The future scope of the research is to investigate microclimate utilizing a mobile weather station attached to a drone for efficient agricultural water management and deep learning-based leaf disease prediction to assist farmers grow their crops with greater efficiency.
12. PUBLISHER’S NOTE
This journal remains neutral with regard to jurisdictional claims in published institutional affiliation.
REFERENCES
1. Wang W, Zhuo L, Li M, Liu Y, Wu P. The effect of development in water-saving irrigation techniques on spatial-temporal variations in crop water footprint and benchmarking. J Hydrol 2019;577:123916. [https://doi.org/10.1016/j.jhydrol.2019.123916]
2. Cemek B, Tasan S, Canturk A, Tasan M, Simsek H. Machine learning techniques in estimation of eggplant crop evapotranspiration. Appl Water Sci 2023;13:136. [https://doi.org/10.1007/s13201-023-01942-1]
3. Han X, Wei Z, Zhang B, Li Y, Du T, Chen H. Crop evapotranspiration prediction by considering dynamic change of crop coefficient and the precipitation effect in back-propagation neural network model. J Hydrol 2021;596:126104. [https://doi.org/10.1016/j.jhydrol.2021.126104]
4. Wang Y, Yin H, Guo X, Zhang W, Li Q. Distributed ANN-bi level two-stage stochastic fuzzy possibilistic programming with Bayesian model for irrigation scheduling management. J Hydrol 2022;606:127435. [https://doi.org/10.1016/j.jhydrol.2022.127435]
5. Zhuo L, Li M, Zhang G, Mekonnen MM, Hoekstra AY, Wada Y, et al. Volume versus value of crop-related water footprints and virtual water flows:A case study for the Yellow River Basin. J Hydrol 2022;608:127674. [https://doi.org/10.1016/j.jhydrol.2022.127674]
6. Zhang C, Li X, Guo P, Huo Z, Huang G. Enhancing irrigation water productivity and controlling salinity under uncertainty:A full fuzzy dependent linear fractional programming approach. J Hydrol 2022;606:127428. [https://doi.org/10.1016/j.jhydrol.2022.127428]
7. Xiang Z, Bailey RT, Kisekka I. Using DSSAT-MODFLOW to determine the controls of groundwater storage and crop yield in groundwater-based irrigated regions. J Hydrol 2022;612:128161. [https://doi.org/10.1016/j.jhydrol.2022.128161]
8. Han X, Zhou Q, Zhang B, Che Z, Wei Z, Qiu R, et al. Real-time methods for short and medium-term evapotranspiration forecasting using dynamic crop coefficient and historical threshold. J Hydrol 2022;606:27414. [https://doi.org/10.1016/j.jhydrol.2021.127414]
9. Meenal R, Boazina PG, Selvakumar AI. Temperature based radiation models for the estimation of global solar radiation at horizontal surface in India. Indian J Sci Technol 2016;9:1-6. [https://doi.org/10.17485/ijst/2016/v9i46/101922]
10. Luo J, Dou X, Ma M. Evaluation of empirical and machine learning approaches for estimating monthly reference evapotranspiration with limited meteorological data in the Jialing River Basin, China. Int J Environ Res Public Health 2022;19:13127. [https://doi.org/10.3390/ijerph192013127]
11. Meenal R,·Binu D, Ramya KC, Michael PA, Kumar KV, Rajasekaran E, et al. Weather forecasting for renewable energy system:A review. Arch Comput Methods Eng 2022;29:2875-91. [https://doi.org/10.1007/s11831-021-09695-3]
12. Chia MY, Huang YF, Koo CH. ANN-Based Reference Evapotranspiration Estimation:Effects of Data Normalization and Parameters Selection. In:Al-Emran M, Al-Sharafi MA, Al-Kabi MN, Shaalan K, editors. Proceedings of International Conference on Emerging Technologies and Intelligent Systems. Lecture Notes in Networks and Systems. Cham:Springer;2022. 322.
13. Meenal R, Selvakumar AI. Assessment of SVM, empirical and ANN based solar radiation prediction models with most influencing input parameters. Renewable Energy 2018;121:324-43. [https://doi.org/10.1016/j.renene.2017.12.005]
14. Vanaja A, Yella VR. Evolution of machine learning in biosciences:A bibliometric network analysis. J Appl Biol Biotechnol 2022;10:45-51. [https://doi.org/10.7324/JABB.2022.100505]
15. Akar F, Katipoglu OM, Yesilyurt SN, Tas MB. Evaluation of tree-based machine learning and deep learning techniques in temperature-based potential evapotranspiration prediction. Pol J Environ Stud 2023;32:1009-23. [https://doi.org/10.15244/pjoes/156927]
16. Katipoglu OM. Combining discrete wavelet decomposition with soft computing techniques to predict monthly evapotranspiration in semi-arid Hakkâri province, Türkiye. Environ Sci Pollut Res Int 2023;30:44043-66. [https://doi.org/10.1007/s11356-023-25369-y]
17. Sarigöl M, Katipoglu OM. Estimation of monthly evaporation values using gradient boosting machines and mode decomposition techniques in the Southeast Anatolia Project (GAP) area in Turkey. Acta Geophys 2023.
18. Meenal R, Michael PA, Pamela D, Rajasekaran E. Weather prediction using random forest machine learning model. Indones J Electr Eng Comput Sci 2021;22:1208-15. [https://doi.org/10.11591/ijeecs.v22.i2.pp1208-1215]
19. Meenal R, Selvakumar AI. Assessment of Solar Energy Potential of Smart Cities of Tamil Nadu using Machine Learning with Big Data. Advances in Big Data and Cloud Computing. Singapore: Springer;2019. 27-36. [https://doi.org/10.1007/978-981-13-1882-5_3]
20. Meenal E, Selvakumar AI, JeyaPrabha SB, Rajasekaran E. Solar mapping of India using support vector machine. J Phys Conf Ser 2018;1142:012010. [https://doi.org/10.1088/1742-6596/1142/1/012010]
21. Hembram P, Suibudhi CR, Subudhi R. Water and irrigation requirement for tomato (Solanum lycopersicum) crop of North central plateau zone of Odisha. J Bio Innov 2020;9:701-10. [https://doi.org/10.46344/JBINO.2020.v09i06.18 https://doi.org/10.46344/JBINO.2020.v09i05.05]
22. Dimitriadou S, Nikolakopoulos KG. Artificial neural networks for the prediction of the reference evapotranspiration of the Peloponnese Peninsula, Greece. Water 2022;14:2027. [https://doi.org/10.3390/w14132027]
23. Hu Z, Bashir RN, Rehman AU, Iqbal SI, Shahid MM, Xu T. Machine learning based prediction of reference evapotranspiration (ET0) using IoT. IEEE Access 2022;10:70526-40. [https://doi.org/10.1109/ACCESS.2022.3187528]
24. Zereg S, Belouz K. Modeling daily reference evapotranspiration using SVR machine learning algorithm with limited meteorological data in Dar-el-Beidha, Algeria. Acta Geophys 2023. [https://doi.org/10.1007/s11600-023-01107-3]
25. Meenal R, Selvakumar AI, Brighta K, Joice SC, Richerd CP. Solar Radiation Resource Assessment using WEKA. In:2nd IEEE International Conference on Inventive Systems and Control (ICISC);2018. p. 1038-42. [https://doi.org/10.1109/ICISC.2018.8398960]
26. Poyen FB, Ghosh A, Kundu P, Hazra S, Sengupta N. Prototype model design of automatic irrigation controller. IEEE Trans Instrum Meas 2021;70:9502217. [https://doi.org/10.1109/TIM.2020.3031760]